Description
在一个 n \times m 的图上,有一条从M到Z的管道,管道分类如下:

‘+’型管道比较特殊,可以垂直和水平传输。如下图所示:
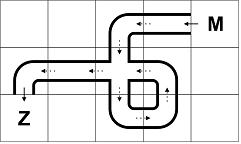
现在这段管道有一个单元格的管道失踪了,请找出缺失管道的位置和它的类型。
题目保证只有一条管道与M和Z相连,图上的所有管道都会被用上,保证答案唯一。
$$1\leq n,m\leq 25$$ 。
Solution
考虑使用 DFS 来解题。
由于数据小,直接从 $$\text{M}$$ 点出发,然后沿着管道走,走到一个没有管道位置就是答案位置,管道类型判断即可。
时间复杂度 $$O(nm)$$ ,具体细节见 代码 部分。
然后这道题就解完了。
考虑使用 模拟 来解题。
用二进制表示出一个管道能否向 上/下/左/右 走,因此对于一个点 $$(x,y)$$ ,可以求出与它相邻的点,从而求出这个点要放的管道要满足什么要求。
$$\text{M}$$ 和 $$\text{Z}$$ 当做 ‘$$+$$’ 号看。
然后还要判断一种情况,读者可以先想想,代码中有。
时间复杂度 $$O(nm)$$ ,具体细节见 代码 部分。
然后这道题目就做完了。
Code
1 | #include<cmath>
|
2 | #include<cstdio>
|
3 | #include<cstring>
|
4 | #include<iostream>
|
5 | #include<algorithm>
|
6 | using namespace std;
|
7 | int n,m,ma[27][27],sx,sy;
|
8 | char s[27][27];
|
9 | void pd(int nx,int ny)
|
10 | {
|
11 | if(ma[nx][ny-1]!=6&&ma[nx][ny-1]!=7&&ma[nx][ny-1]!=1&&ma[nx][ny-1]!=2&&ma[nx][ny+1]!=6&&ma[nx][ny+1]!=7&&ma[nx][ny+1]!=3&&ma[nx][ny+1]!=4)
|
12 | printf("|");
|
13 | else if(ma[nx-1][ny]!=5&&ma[nx-1][ny]!=7&&ma[nx-1][ny]!=1&&ma[nx-1][ny]!=4&&ma[nx+1][ny]!=5&&ma[nx+1][ny]!=7&&ma[nx+1][ny]!=2&&ma[nx+1][ny]!=3)
|
14 | printf("-");
|
15 | else if(ma[nx-1][ny]!=5&&ma[nx-1][ny]!=7&&ma[nx-1][ny]!=1&&ma[nx-1][ny]!=4&&ma[nx][ny-1]!=6&&ma[nx][ny-1]!=7&&ma[nx][ny-1]!=1&&ma[nx][ny-1]!=2)
|
16 | printf("1");
|
17 | else if(ma[nx][ny-1]!=6&&ma[nx][ny-1]!=7&&ma[nx][ny-1]!=1&&ma[nx][ny-1]!=2&&ma[nx+1][ny]!=5&&ma[nx+1][ny]!=7&&ma[nx+1][ny]!=2&&ma[nx+1][ny]!=3)
|
18 | printf("2");
|
19 | else if(ma[nx+1][ny]!=5&&ma[nx+1][ny]!=7&&ma[nx+1][ny]!=2&&ma[nx+1][ny]!=3&&ma[nx][ny+1]!=6&&ma[nx][ny+1]!=7&&ma[nx][ny+1]!=3&&ma[nx][ny+1]!=4)
|
20 | printf("3");
|
21 | else if(ma[nx-1][ny]!=5&&ma[nx-1][ny]!=7&&ma[nx-1][ny]!=1&&ma[nx-1][ny]!=4&&ma[nx][ny+1]!=6&&ma[nx][ny+1]!=7&&ma[nx][ny+1]!=3&&ma[nx][ny+1]!=4)
|
22 | printf("4");
|
23 | else
|
24 | printf("+");
|
25 | }
|
26 | void dfs(int nx,int ny,int tou)
|
27 | {
|
28 | if(ma[nx][ny]==-1)
|
29 | return;
|
30 | else if(ma[nx][ny]==1)
|
31 | if(tou==1)
|
32 | dfs(nx,ny+1,4);
|
33 | else
|
34 | dfs(nx+1,ny,2);
|
35 | else if(ma[nx][ny]==2)
|
36 | if(tou==2)
|
37 | dfs(nx,ny+1,4);
|
38 | else
|
39 | dfs(nx-1,ny,1);
|
40 | else if(ma[nx][ny]==3)
|
41 | if(tou==2)
|
42 | dfs(nx,ny-1,3);
|
43 | else
|
44 | dfs(nx-1,ny,1);
|
45 | else if(ma[nx][ny]==4)
|
46 | if(tou==1)
|
47 | dfs(nx,ny-1,3);
|
48 | else
|
49 | dfs(nx+1,ny,2);
|
50 | else if(ma[nx][ny]==5)
|
51 | if(tou==1)
|
52 | dfs(nx-1,ny,1);
|
53 | else
|
54 | dfs(nx+1,ny,2);
|
55 | else if(ma[nx][ny]==6)
|
56 | if(tou==3)
|
57 | dfs(nx,ny-1,3);
|
58 | else
|
59 | dfs(nx,ny+1,4);
|
60 | else if(ma[nx][ny]==7)
|
61 | if(tou==1)
|
62 | dfs(nx-1,ny,1);
|
63 | else if(tou==2)
|
64 | dfs(nx+1,ny,2);
|
65 | else if(tou==3)
|
66 | dfs(nx,ny-1,3);
|
67 | else
|
68 | dfs(nx,ny+1,4);
|
69 | else if(ma[nx][ny]==0)
|
70 | {
|
71 | printf("%d %d ",nx,ny);
|
72 | pd(nx,ny);
|
73 | return;
|
74 | }
|
75 | }
|
76 | int main()
|
77 | {
|
78 | scanf("%d%d\n",&n,&m);
|
79 | for(int i=1;i<=n;i++)
|
80 | {
|
81 | scanf("%s",s[i]+1);
|
82 | for(int j=1;j<=m;j++)
|
83 | {
|
84 | if(s[i][j]=='|')
|
85 | ma[i][j]=5;
|
86 | else if(s[i][j]=='-')
|
87 | ma[i][j]=6;
|
88 | else if(s[i][j]=='+')
|
89 | ma[i][j]=7;
|
90 | else if(s[i][j]=='1')
|
91 | ma[i][j]=1;
|
92 | else if(s[i][j]=='2')
|
93 | ma[i][j]=2;
|
94 | else if(s[i][j]=='3')
|
95 | ma[i][j]=3;
|
96 | else if(s[i][j]=='4')
|
97 | ma[i][j]=4;
|
98 | else if(s[i][j]=='M')
|
99 | ma[i][j]=-1,sx=i,sy=j;
|
100 | else if(s[i][j]=='Z')
|
101 | ma[i][j]=-1;
|
102 | }
|
103 | }
|
104 | if(ma[sx-1][sy]==5||ma[sx-1][sy]==1||ma[sx-1][sy]==4||ma[sx-1][sy]==7)
|
105 | {
|
106 | dfs(sx-1,sy,1);
|
107 | }
|
108 | else if(ma[sx+1][sy]==5||ma[sx+1][sy]==2||ma[sx+1][sy]==3||ma[sx+1][sy]==7)
|
109 | {
|
110 | dfs(sx+1,sy,2);
|
111 | }
|
112 | else if(ma[sx][sy-1]==6||ma[sx][sy-1]==1||ma[sx][sy-1]==2||ma[sx][sy-1]==7)
|
113 | {
|
114 | dfs(sx,sy-1,3);
|
115 | }
|
116 | else if(ma[sx][sy+1]==6||ma[sx][sy+1]==3||ma[sx][sy+1]==4||ma[sx][sy+1]==7)
|
117 | {
|
118 | dfs(sx,sy+1,4);
|
119 | }
|
120 | return 0;
|
121 | }
|
1 | #include <cstdio>
|
2 | int st[101][101];
|
3 | int To[8]={0,5,9,10,6,12,3,15};
|
4 | int Guan[16]={0,0,0,6,0,1,4,0,0,2,3,0,5,0,0,7};
|
5 | char ma[101][101];
|
6 | int change(char x)
|
7 | {
|
8 | if(x>='1' && x<='4')
|
9 | {
|
10 | return x-'0';
|
11 | }
|
12 | else if(x=='|')
|
13 | {
|
14 | return 5;
|
15 | }
|
16 | else if(x=='-')
|
17 | {
|
18 | return 6;
|
19 | }
|
20 | else if(x=='+')
|
21 | {
|
22 | return 7;
|
23 | }
|
24 | else if(x=='M')
|
25 | {
|
26 | return 7;
|
27 | }
|
28 | else if(x=='Z')
|
29 | {
|
30 | return 7;
|
31 | }
|
32 | return 0;
|
33 | }
|
34 | char change2(int x)
|
35 | {
|
36 | if(x>=1 && x<=4)
|
37 | {
|
38 | return x+'0';
|
39 | }
|
40 | else if(x==5)
|
41 | {
|
42 | return '|';
|
43 | }
|
44 | else if(x==6)
|
45 | {
|
46 | return '-';
|
47 | }
|
48 | else if(x==7)
|
49 | {
|
50 | return '+';
|
51 | }
|
52 | return -1;
|
53 | }
|
54 | int main()
|
55 | {
|
56 | int n=0,m=0;
|
57 | scanf("%d %d",&n,&m);
|
58 | for(int i=1;i<=n;i++)
|
59 | {
|
60 | scanf("%s",ma[i]+1);
|
61 | for(int j=1;j<=m;j++)
|
62 | {
|
63 | st[i][j]=change(ma[i][j]);
|
64 | }
|
65 | }
|
66 | int ansx=0,ansy=0;
|
67 | char ansc;
|
68 | for(int i=1;i<=n;i++)
|
69 | {
|
70 | for(int j=1;j<=m;j++)
|
71 | {
|
72 | if(st[i][j]!=0)
|
73 | {
|
74 | continue;
|
75 | }
|
76 | int t=0;
|
77 | int nx=0,ny=0;
|
78 | nx=i-1,ny=j;
|
79 | if(nx>=1 && nx<=n && ny>=1 && ny<=m)
|
80 | {
|
81 | if((To[st[nx][ny]] & 4))
|
82 | {if(i==6 && j==5)
|
83 | {
|
84 | printf("a\n");
|
85 | }
|
86 | t+=8;
|
87 | }
|
88 | }
|
89 |
|
90 | nx=i+1,ny=j;
|
91 | if(nx>=1 && nx<=n && ny>=1 && ny<=m)
|
92 | {
|
93 | if((To[st[nx][ny]] & 8))
|
94 | {
|
95 | t+=4;
|
96 | }
|
97 | }
|
98 |
|
99 | nx=i,ny=j-1;
|
100 | if(nx>=1 && nx<=n && ny>=1 && ny<=m)
|
101 | {
|
102 | if((To[st[nx][ny]] & 1))
|
103 | {
|
104 | t+=2;
|
105 | }
|
106 | }
|
107 |
|
108 | nx=i,ny=j+1;
|
109 | if(nx>=1 && nx<=n && ny>=1 && ny<=m)
|
110 | {
|
111 | if((To[st[nx][ny]] & 2))
|
112 | {
|
113 | t+=1;
|
114 | }
|
115 | }
|
116 | if(Guan[t])
|
117 | {
|
118 | if(ma[i-1][j]!='M' && ma[i-1][j]!='Z' && ma[i+1][j]!='M' && ma[i+1][j]!='Z' && ma[i][j-1]!='M' && ma[i][j-1]!='Z' && ma[i][j+1]!='M' && ma[i][j+1]!='Z')
|
119 | {
|
120 | printf("%d %d %c",i,j,change2(Guan[t]));
|
121 | return 0;
|
122 | }
|
123 | else
|
124 | {
|
125 | ansx=i,ansy=j,ansc=change2(Guan[t]);
|
126 | }
|
127 | }
|
128 | }
|
129 | }
|
130 | printf("%d %d %c",ansx,ansy,ansc);
|
131 | return 0;
|
132 | }
|