- 例子(已被授予主人公的名字使用权)
ZZJ 进入了一个 n × m 的迷宫矩阵,执着的他表示要穿过迷宫。
ZZJ 在地图的左上角,而迷宫出口在右下角,设进入每个房间都需要 1 的时间,他在入口的地面上捡到一张迷宫地图,发现有一些障碍物(图中以“障碍”表示,代码中以“#”表示,存在map数组中),于是他决定计算出自己到终点最少需要时间(请思考后再往下看)。
| \ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 起点 | ||||||
| 2 | 障碍 | ||||||
| 3 | 障碍 | ||||||
| 4 | 障碍 | ||||||
| 5 | 障碍 | 终点 |
ZZJ 进入了一个 n × m 的迷宫矩阵,执着的他表示要穿过迷宫。
ZZJ 在地图的左上角,而迷宫出口在右下角,设进入每个房间都需要 1 的时间,他在入口的地面上捡到一张迷宫地图,发现有一些障碍物(图中以“障碍”表示,代码中以“#”表示,存在map数组中),于是他决定计算出自己到终点最少需要时间(请思考后再往下看)。
| \ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 起点 | ||||||
| 2 | 障碍 | ||||||
| 3 | 障碍 | ||||||
| 4 | 障碍 | ||||||
| 5 | 障碍 | 终点 |
一个 $2^n \times2^n$ 的矩阵,每个位置站着一个作弊者,每次将正方形矩阵 分割 成4个更小的正方形矩阵,每个矩阵的边长是原矩阵的 一半 。其中 左上角 那一个矩阵的所有作弊者都将得到 赦免 ,剩下的三个矩阵中,每一个矩阵继续分为 4 个更小的矩阵,然后以 同样的方式 分割矩阵,以同样的方式 赦免 ,直到矩阵不能再分割为止,剩下的作弊者将会被惩罚。求这个矩阵每个作弊者的命运,赦免为 0 ,惩罚为 1 。
$n\leq 10$
给你起点和终点的三维坐标 $(s_x,s_y,s_z)$ 和 $(e_x,e_y,e_z)$ ,以及 $n$ 个球的球心的三维坐标 $(x_i,y_i,z_i)$ 和星域的半径 $r_i$ 。现在要从起点到终点,在一个球内穿梭不需要时间,你的速度是 $0.1$ ,现在请你求出从起点到终点所需的最短时间,结果取整到最近的整数,输入数据保证取整是明确的。
$0 \leq n \leq 100,0 \leq |x_i|,|y_i|,|z_i|,r_i\leq 10^4$ 。
定义新运算 “$!$” ,运算规则如下:
$a!b = a!(b-1) \times (a-1)!b ( a > 0,b > 0 )$
$a!b = 1 ( a = 0 )$
$a!b = a ( b = 0 )$
。
给你两个正整数 $n$ 和 $k$ ,现在请你求出 $n!k$ 的因子个数 $\mod (10^9+9)$ 。
$1\leq n\leq 1000,1 \leq k \leq 100$ 。
开始有一初始数列 $a=[a_{1},a_{2},a_{3},···,a_{n}]$ ,定义 $f(a,k)=[a_{2},a_{3},···,a_{k},a_{1},a_{k+2},a_{k+3},···,a_{2k},a_{k+1}···]$ ,也就是把 $a$ 分段,每段 $k$ 个,若最后不足 $k$ 个时,将剩下的组成新的一段,每段第一个移成该段最后一个。
求 $f(f(f(f(f(1,2,3,···,n),2),3),···),n)$ 的结果。
$1\leq n\leq 10^{6}$ 。
给你一个正整数 $n$ ,然后给你 $n$ 个正整数 $a_1$ ~ $a_n$ ,问你是否有可能存在入栈顺序为 $1,2,3,…,n$ ,出栈顺序为 $a_1$ ~ $a_n$ 的情况,共有 $T$ 组数据。
$1 \leq n \leq 1000,1 \leq T \leq 10$ 。
给你一个正整数 $n$ 和一个 $n \times n$ 的矩阵 $a$,有两个人轮流对这个矩阵进行操作,每次可以删掉最后一行或最后一列,但必须要保证所删的行或列的和是偶数。当一个人无法操作时这个人就输了。
现在请你求出在双方都使用最优策略的情况下,先手是否有必胜策略,有则输出 $W$ ,否则输出 $L$ 。
$1 \leq n \leq 1000,1 \leq T \leq 5$ 。
$\text{保证每一行或每一列的和不会超过};2 \times 10^9$ 。
在一个 n \times m 的图上,有一条从M到Z的管道,管道分类如下:

‘+’型管道比较特殊,可以垂直和水平传输。如下图所示:
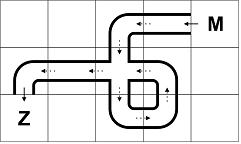
现在这段管道有一个单元格的管道失踪了,请找出缺失管道的位置和它的类型。
题目保证只有一条管道与M和Z相连,图上的所有管道都会被用上,保证答案唯一。
$$1\leq n,m\leq 25$$ 。
有两个长度为 $n$ 的数组 $s[]$ 和 $b[]$ 。
现在有一个长度为 $n$ 的并且只含有 0 和 1 并且至少有一个 $1$ 的数组 $k[]$ ,使得 $|\prod_{i=1}^{n}s_ik_i-\sum_{i=1}^{n}b_ik_i|$ 的值最小。
现在请你求出这个最小值。
$1\leq n\leq 10,\prod_{i=1}^{n}s_i,\sum_{i=1}^{n}b_i\leq 10^{9}$ 。
